Deep Learning 17 优化目标

[TOC]

优化目标

概念区分

1、整体理解：损失函数，代价函数，目标函数，熵=>都是最优化问题下的的优化目标，通过设定优化目标获取最优化问题的最优解

2、设计原理：为什么要设计这样的优化目标

• 用交叉熵的原因，交叉熵和KL散度的关系
• 用平方损失的原因，平方损失和最大似然的关系
• 添加正则子的原因，为什么能添加这样的正则子

回归问题

平方「Square」

平方根「Square Root」

分类问题-熵「Entropy」

与熵相关的为信息论相关内容

熵「Entropy」

信息量

事件A的自信息量，A这个事件包含了多少信息

$s(x)=\sum_{i}P_A(x_i)log(P_A(x_i))\$

验证：

交叉熵「Cross Entropy」

分类问题-二分类，对数似然

事件AB，从A的角度看，如何描述B

信息论公式：

$H(A,B)=-\sum_{i}P_A(x_i)log(P_B(x_i))\$

对于样本集上的数据，两种表达形式，单个样本Loss & 整个样本集然后除样本数Cost

Loss => $L=yln\hat{y}+(1-y)ln(1-\hat{y})$​

Cost => $C=-\frac{1}{n}\sum_{x}^{}[yln\hat{y}+(1-y)ln(1-\hat{y}]\$

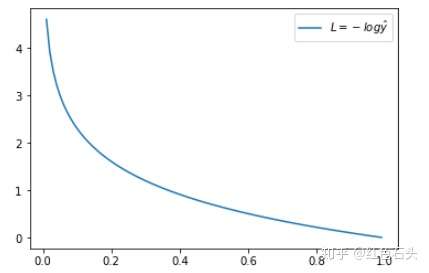
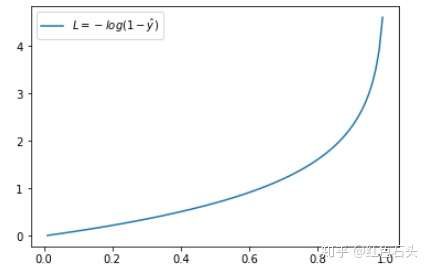
验证：当真实$y=1$，如果$\hat{y}$越接近1，则损失函数Loss越小；如果$\hat{y}$越接近0，则损失函数Loss越大。因而达到忘Loss损失函数变小的方向变化。（当真实$y=0$亦然，看下图左边是$y=1$的情况，右边是$y=0$的情况）

多分类交叉熵「Categorical Cross Entropy」

分类问题-多分类，对数似然

相对熵「Relative Entropy」

衡量两个分布的不同

事件AB，从A的角度看，B有多大不同

$D_{KL}(A|B)=\sum_{i}P_A(x_i)log(P_A(x_i))-\sum_{i}P_A(x_i)log(P_B(x_i))\$ （对于离散事件是求和，对于连续事件是求积分）

相对熵包含了交叉熵的内容，$D_{KL}(A|B)=\sum_{i}P_A(x_i)log(P_A(x_i))-\sum_{i}P_A(x_i)log(P_B(x_i))=s(A)+H(A,B)\$，也就是相对熵=坐标系自己的熵+交叉熵

验证：由于坐标系选取不同，对于事件A和事件B，从A的角度看，$D_{KL}(A|B)\neq D_{KL}(B|A)$

交叉熵VS相对熵/KL散度

一般情况下，都用交叉熵，不用KL散度。

首先理解分类问题的目标 =>看模型学习到的分布P(model)和真实分布P(real)是否接近 =>看模型学习到的分布P(model)和训练数据P(training)的分布是否接近 =>因而可以用KL散度来进行计算$D_{KL}(P(training)|P(model))$ =>将KL散度进行展开$D_{KL}(P(training)|P(model))=s(P(training))+H(P(training),P(model))$ =>由于训练数据固定，那么对应的训练数据的熵也是不变的，所以$D_{KL}$等价于交叉熵，而因为交叉熵方便计算，所以一般都使用交叉熵